Introduction to Geometric Congruence
Geometry, a branch of mathematics that dates back to ancient times, involves the study of shapes, sizes, properties of space, and relative position of figures. Among its essential concepts is the idea of congruence.
The concept of congruence is akin to a perfect match or coincidence in the real world. In the universe of geometry, it describes the scenario where two geometric figures have the same shape and size. This leads us to an exciting expedition: figuring out “which pair of triangles can be proven congruent by SAS?” To answer this, let’s first understand the essence of triangles.
The Essence of Triangles
Triangles are among the simplest and most fundamental geometric shapes, but they hold a vast array of complexities and subtleties. Defined by three straight sides and three angles, they serve as building blocks for understanding more complex shapes.
What Defines Congruence in Triangles?
When it comes to triangles, congruence means that they have identically matched sides and angles. Essentially, if you can “pick up” one triangle, flip it, rotate it or move it so that it lays perfectly on the other triangle, they are congruent. Now, let’s dig into the tools used to establish congruence, known as postulates and theorems.
Postulates and Theorems in Geometry
Postulates, also known as axioms, are statements that are accepted as true without proof. On the other hand, theorems are statements that require proof, often built on previously established postulates and theorems. In the context of triangle congruence, several postulates and theorems come into play, including Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) for right triangles. Today, we focus on the SAS postulate.
An Introduction to the SAS Postulate
The SAS postulate, short for Side-Angle-Side, is a rule used to prove whether a pair of triangles are congruent. The SAS postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.
The Mechanics of SAS: Side-Angle-Side
To better understand the SAS postulate, visualize a pair of triangles. Start with two sides of a triangle. If they are equal in length to two sides of another triangle, and the angle formed by these two sides is also equal in both triangles, the SAS postulate says that these triangles are congruent. Remember, the term “included angle” means the angle formed between the two sides being considered.
Necessary Conditions for SAS Congruence
The SAS postulate seems straightforward, but there are specific conditions that must be met for it to apply. The two pairs of sides that are being compared must be equal in length, and the angle formed by these sides (the included angle) must also be the same in both triangles. If these conditions aren’t met, then the SAS postulate cannot be applied, and the triangles cannot be considered congruent.
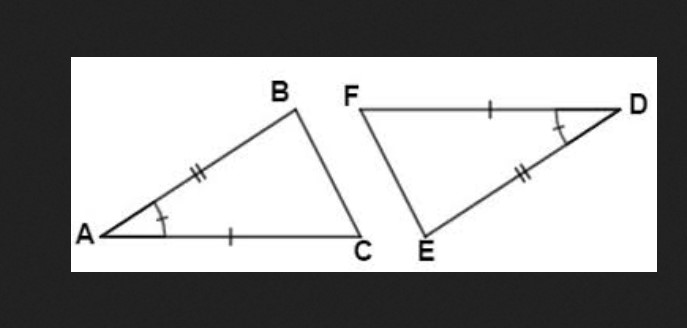
Which Pair of Triangles Can Be Proven Congruent by SAS
Returning to our central question, “which pair of triangles can be proven congruent by SAS?”, the answer lies in the application of the SAS postulate. Any pair of triangles that meet the conditions set by this postulate can be proven congruent by SAS. Specifically, if two sides and the included angle of one triangle are equal in measurement to two sides and the included angle of another triangle, these two triangles are congruent by the SAS postulate.
Examples of SAS Triangle Congruence
To illustrate, let’s consider two triangles, ABC and DEF. If side AB equals side DE, side BC equals side EF, and angle ABC equals angle DEF, then triangle ABC is congruent to triangle DEF by the SAS postulate.
Real-world Applications of SAS Congruence
Believe it or not, the SAS postulate extends beyond the classroom. Engineers, architects, and computer graphics designers, to name a few, routinely apply the SAS postulate and other geometric principles in their work.
Common Misconceptions about SAS Congruence
One common misconception about the SAS postulate is that it can apply when the angle is not included. This is incorrect. The “A” in SAS must represent the included angle between the two sides.
SAS vs. Other Congruence Postulates
There are other postulates used to prove triangle congruence, including SSS, ASA, and HL. Each has its own conditions and applications, but none can be used interchangeably with SAS.
Testing for Congruence: SAS Method
Applying the SAS method to prove triangle congruence involves measuring two sides and the included angle. If these measurements are identical between two triangles, congruence is established.
Importance of Order in SAS Congruence
In the SAS postulate, the order matters. Side-angle-side means that the angle is between the two sides. If the angle is not between the sides, the postulate doesn’t apply.
Impact of SAS on Geometric Proofs
SAS plays a crucial role in geometric proofs, allowing us to demonstrate the congruence of triangles without measuring all sides and angles. This greatly simplifies the process of proving geometric relations and properties.
Role of SAS in Advanced Mathematics
The SAS postulate is not just limited to geometry. Its principles are also found in more advanced mathematical fields, such as trigonometry and calculus.
Understanding Congruence Through SAS: A Summary
In essence, understanding the SAS postulate helps one comprehend the fundamental idea of congruence in geometry. By knowing “which pair of triangles can be proven congruent by SAS,” we gain a deeper appreciation of the symmetry and balance inherent in the geometric world.
FAQs on SAS and Triangle Congruence
What does SAS mean in triangle congruence?
SAS stands for Side-Angle-Side. It’s a postulate used to prove the congruence of two triangles. If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then these two triangles are congruent.
Can SAS be applied to non-triangular shapes?
The SAS postulate is specific to triangles. It does not apply to other geometric shapes.
Why is the included angle important in the SAS postulate?
The included angle is crucial in the SAS postulate as it is the angle formed by the two sides being compared. Without this specific angle, we cannot apply the SAS postulate.
Is the SAS postulate universally accepted?
Yes, the SAS postulate is universally accepted in geometry as a valid method to prove triangle congruence.
How does SAS relate to other congruence postulates?
SAS, like other congruence postulates (SSS, ASA, HL), provides a specific set of conditions under which triangle congruence can be proven. However, the conditions for each postulate are different.
Can the SAS postulate be proven?
The SAS postulate, like all postulates, is accepted as an unproven truth. It serves as a fundamental building block for proving other geometric theorems.
Conclusion
The world of geometry offers us an intriguing perspective on the abstract side of mathematics. By understanding the intricacies of concepts like the SAS postulate and congruence, we deepen our comprehension of the world around us. Next time you look at a pair of triangles, think about the conditions that might make them congruent. Remember the SAS postulate and use it as a tool to see the world through a geometric lens.